Na początek nieco określeń teoretycznych, które poprzez swoje skomplikowanie często wywołują albo uśmiech albo zirytowanie na twarzy czytającego. Niemniej kilka definicji podstawowych jest dla wprowadzenia do tej tematyki niezbędnych. Uniknę w dalszej części artykułu od wykładania podstaw teorii matematycznej, na rzecz zaprezentowania praktycznego podejścia do tych zagadnień. Dlatego przy omawianiu kluczowych momentów działania sieci ograniczę się do zaprezentowania tylko kilku wzorów absolutnie niezbędnych na rzecz fragmentów algorytmów z konkretną implementacją pierwowzoru matematycznego.
a) Sztuczne sieci Neuronowe (SSN)
Poprzez nazwę Sztuczne Sieci Neuronowe (SSN) określa się najczęściej programowe lub sprzętowe symulatory modeli matematycznych, realizujące (pseudo-)równoległe przetwarzanie informacji, składające się z wielu wzajemnie połączonych funktorów zwanych poprzez analogię ze swoimi biologicznymi protoplastami – neuronami. Emulują one niektóre spośród zaobserwowanych właściwości biologicznych układów nerwowych oraz bazują na analogii adaptacyjnego uczenia biologicznego. Odnosząc tę definicję do architektury połączeń, równoległego przetwarzania i systemów neuromorficznych, sztuczne sieci neuronowe są swoistym systemem inspirowanym przez to, w jaki sposób gęsto połączone między sobą struktury mózgu obrabiają dane, w różny sposób docierające z otoczenia. Kluczowym elementem SSN jest zatem nowatorska struktura systemu przetwarzania informacji. System taki składa się z dużej liczby rozlegle połączonych ze sobą elementów przetwarzających, które – jak wspomniano wyżej – są analogiczne do biologicznych neuronów i powiązane ze sobą ważonymi połączeniami, które są znowu analogiczne do biologicznych synaps. SSN są podzbiorem rozwiązań nazywanych AI Artifical Inteligence – sztuczna inteligencja. Ich dynamiczny rozwój nastąpił dopiero od drugiej połowy lat 80, w wyniku możliwości jakie dała współczesna informatyka i elektronika.
Podstawową cechą różniącą SSN od programów realizujących algorytmiczne przetwarzanie informacji jest zdolność generalizacji czyli umiejętność uogólniania wiedzy dla nowych wzorców nieznanych wcześniej, czyli nie prezentowanych w trakcie nauki. Określa się to także jako zdolność SSN do aproksymacji wartości funkcji wielu zmiennych w przeciwieństwie do interpolacji możliwej do otrzymania przy przetwarzaniu algorytmicznym. Można to ująć jeszcze inaczej. Np. systemy ekspertowe z reguły wymagają zgromadzenia i bieżącego dostępu do całej wiedzy na temat zagadnień, o których będą rozstrzygały. SSN wymagają natomiast jednorazowego nauczenia, przy czym wykazują one tolerancję na nieciągłości, przypadkowe zaburzenia lub wręcz braki w zbiorze uczącym. Pozwala to na zastosowanie ich tam, gdzie nie da się rozwiązać danego problemu w żaden inny, efektywny sposób.
Uczenie w systemach biologicznych prawdopodobnie zmienia ustawienia w połączeniach synaptycznych, znajdujących się pomiędzy neuronami.
Uczenie SSN natomiast zmienia liczbowe wartości wag znajdujących się również pomiędzy neuronami. Uczenie zatem zachodzi poprzez bezpośrednią ekspozycję rzeczywistego zestawu danych, gdzie algorytm uczący modeluje wagi połączeń.
Te właśnie wagi połączeń mają „zapisane” dane niezbędne do rozwiązywania specyficznych problemów. Pomimo pojawienia się SSN w późnych latach 50, dopiero w połowie 80 stały się wystarczająco dojrzałe do zastosowania w poważnych aplikacjach. Dzisiaj SSN są stosowane do wzrastającej liczby problemów świata rzeczywistego o znacznym stopniu zawiłości. Wiele skutecznych predykcji uzyskanych za pomocą SSN opiera się na prezentacji ciągów uczących wygenerowanych z danych historycznych.
b) Zastosowanie SSN
SSN oferują idealne rozwiązania dla dużego zakresu klasyfikowanych problemów (jak np.: mowa, rozpoznawanie znaków i sygnałów) równie dobrze jak predykcja i modelowanie systemów, gdzie procesy (fizyczne, ekonomiczne, …) są niezrozumiałe bądź bardzo skomplikowane. SNN mogą być stosowane do nadzoru nad procesami przebiegającymi w czasie rzeczywistym, gdzie zmienne wejściowe są odczytami pomiarów używanymi do sterowania on-line, a sieć uczy się funkcji kontroli.
SSN sprawdzają się także w rozwiązywaniu problemów, które są zbyt skomplikowane dla konwencjonalnych technologii (np. problemy, które nie mają rozwiązania algorytmicznego, bądź takowe jest zbyt skomplikowane do znalezienia), sprawdzają się też dobrze tam, gdzie ludzie nie są w stanie zastosować tradycyjnych metod.
W świecie finansów wszystko, co przynosi nawet minimalną przewagę nad konkurencją, może oznaczać miliony dodatkowego zysku. Ze względu na opisane powyżej specyficzne cechy i niepodważalne zalety, obszar zastosowań sieci neuronowych jest rozległy:
- Rozpoznawanie wzorców (znaków, liter, kształtów, sygnałów mowy, sygnałów sonarowych),
- Klasyfikowanie obiektów,
- Prognozowanie i ocena ryzyka ekonomicznego,
- Prognozowanie zmian cen rynkowych (giełdy, waluty),
- Ocena zdolności kredytowej,
- Ocena wniosków ubezpieczeniowych,
- Rozpoznawanie wzorów podpisów,
- Prognozowanie zapotrzebowania na energię elektryczną,
- Diagnostyka medyczna,
- Dobór pracowników,
- Prognozowanie sprzedaży,
- Analizowanie zachowań klienta w supermarketach,
- Aproksymowanie wartości funkcji,
- i zapewne wiele innych.
Wielowarstwowe nieliniowe sztuczne sieci neuronowe
Tematem poruszonym niżej są wielowarstwowe nieliniowe sztuczne sieci neuronowe jednokierunkowe uczone metodą wstecznej propagacji błędów multilayer non-linear artifical neural nets with backpropagation – realizowane programowo. Nazwa ta jest tylko z pozoru szalona, gdyż poszczególne jej człony opisują po prostu funkcje zgodnie ze swoją nazwą
a) Neuron
Podstawowym elementem składowym sieci neuronowej jest: neuron. Jego schemat został opracowany przez McCullocha i Pittsa w 1943 roku i oparty został na budowie biologicznej komórki nerwowej.
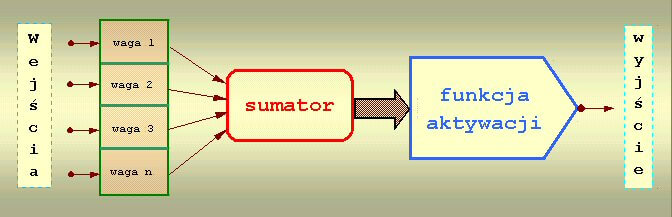
Działanie jest następujące: do wejść doprowadzane są sygnały dochodzące z wejść sieci lub neuronów warstwy poprzedniej. Każdy sygnał mnożony jest przez odpowiadającą mu wartość liczbową zwaną wagą. Wpływa ona na percepcję danego sygnału wejściowego i jego udział w tworzeniu sygnału wyjściowego przez neuron. Waga może być pobudzająca – dodatnia lub opóźniająca – ujemna; jeżeli nie ma połączenia między neuronami to waga jest równa zero. Zsumowane iloczyny sygnałów i wag stanowią argument funkcji aktywacji neuronu. W tym miejscu warto porównać model neuronu realizowany programowo z jego odpowiednikiem elektronicznym zrealizowanym na elementach dyskretnych.
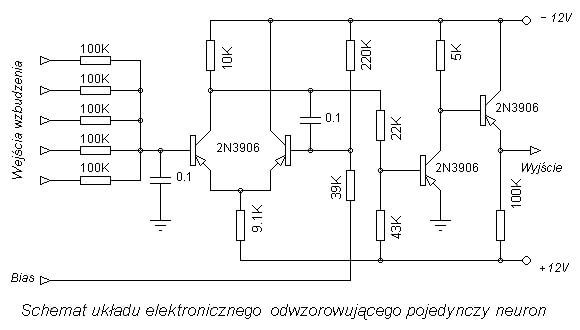
Wejścia wzbudzenia odpowiadają dendrytom a Bias – neurytowi. Długość impulsu układu – około 6 ms, czas całkowania układu – 2 ms, czas regeneracji – około 10 ms (odpowiada to w przybliżeniu stałym czasowym żywej komórki nerwowej, z wyjątkiem długości impulsu – ten w żywej komórce jest krótszy). Dla odwzorowania prostych funkcji wzroku do wejść układu podłącza się elementy fotoelektryczne. Umożliwia to zademonstrowanie zjawiska scalania obrazów impulsowych przez narząd wzroku, co jest praktycznie wykorzystywane w kinie i telewizji, a także – zjawiska wzajemnego hamowania komórek w jednej sieci (występuje to u niektórych zwierząt i polega na tym, że komórka odtwarzająca bodźce świetlne o większej intensywności hamuje wyzwalanie impulsów komórek sąsiednich; dzięki temu zwiększa się lokalnie kontrastowość układu i zwierzę widzi wyraźniej). Szeregowe połączenie takich komórek stanowi przybliżoną analogię włókien nerwowych.
b) Funkcja aktywacji
Wartość funkcji aktywacji jest sygnałem wyjściowym neuronu i propagowana jest do neuronów warstwy następnej. Funkcja aktywacji przybiera jedną z trzech postaci:
- nieliniowa
- liniowa
- skoku jednostkowego tzw. funkcja progowa
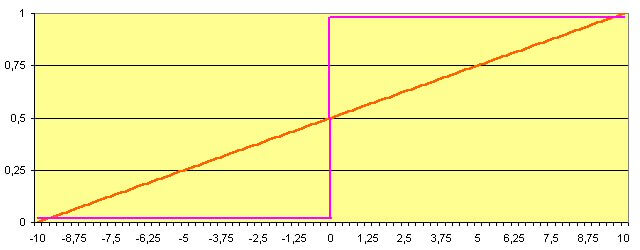
rysunek 3: funkcja aktywacji liniowa i skoku jednostkowego
Wybór funkcji aktywacji zależy od rodzaju problemu jaki stawiamy przed siecią do rozwiązania. Dla sieci wielowarstwowych najczęściej stosowane są funkcje nieliniowe, gdyż neurony o takich charakterystykach wykazują największe zdolności do nauki, polegające na możliwości odwzorowania w sposób płynny dowolnej zależności pomiędzy wejściem a wyjściem sieci. Umożliwia to otrzymanie na wyjściu sieci informacji ciągłej a nie tylko postaci: TAK – NIE.
Wymagane cechy funkcji aktywacji to:
- ciągłe przejście pomiędzy swoją wartością maksymalną a minimalną (np. 0-1),
- łatwa do obliczenia i ciągła pochodna,
- możliwość wprowadzenia do argumentu parametru beta do ustalania kształtu krzywej.
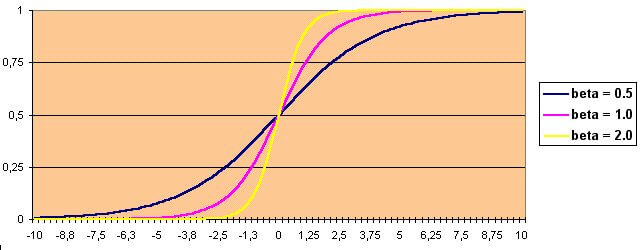
Najczęściej stosowanymi są funkcje: sigmoidalna zwana też krzywą logistyczną (o charakterze unipolarnym; przyjmuje ona wartości pomiędzy 0 a 1) oraz tangens hiperboliczny (o charakterze bipolarnym; wartości pomiędzy -1 a 1). Oczywiście każdą z nich można przeskalować tzn. sigmoidę do bipolarnej a tangensoidę do unipolarnej. Inne, rzadziej używane nieliniowe funkcje aktywacji neuronu to: sinusoida i cosinusoida (ograniczone do odcinków odpowiednio 1,5 Pi do 2,5 Pi oraz Pi do 2 Pi przyjmując wartości pomiędzy 0 a 1).

Tabela 1: wzory wybranych nieliniowych funkcji aktywacji i ich pochodnych
Zaprezentowane powyżej funkcje aktywacji charakteryzują się tym, że wartość pochodnej oblicza się z obliczonej wartości funkcji. W sieci neuronowej możemy rozróżnić kilka rodzajów neuronów:
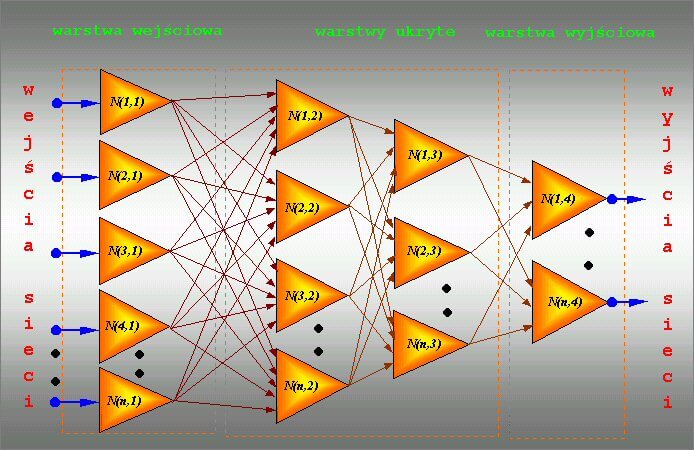
- warstwy wejściowej
- warstw ukrytych
- warstwy wyjściowej
z tym, że jest to podział bardziej formalny niż merytoryczny, gdyż różnice funkcjonalne pomiędzy tymi typami raczej nie występują. Można natomiast stosować w różnych warstwach różne funkcje aktywacji i współczynniki beta.
Analizując budowę i zasadę działania pojedynczego neuronu można uznać go za swego rodzaju prosty procesor, który posiada pamięć (wartości wagowe) i możliwości przetworzenia danych (funkcja aktywacji). Pojemność informacyjna pojedynczego neuronu nie jest duża. Jej powiększenie, a przez to zwiększenie zdolności przetwarzania uzyskuje się poprzez odpowiednie połączenie wielu neuronów. Powstaje wówczas sieć wielowarstwowa
Ten typ sieci cieszy się największym zainteresowaniem. Nazywana jest czasem perceptronem wielowarstwowym. Jej cechą charakterystyczną jest występowanie co najmniej jednej warstwy ukrytej neuronów, pośredniczącej w przekazywaniu sygnałów pomiędzy wejściami a wyjściami sieci.
c) Rozpoznawanie wzorców
Co można uznać za wzorzec ? Wzorcem może być zeskanowany obraz litery przy rozpoznawaniu znaków, przy czym litera może być drukowana lub pisana ręcznie – np. do automatycznego rozpoznawania kodów pocztowych na listach. Wzorcem może być kształt części maszyny w fabryce wykorzystującej automaty, które muszą w odpowiedni sposób ją złapać w procesie produkcyjnym. Wzorcem może być sygnał akustyczny wytwarzany przez śrubę napędową okrętu podwodnego albo formacja w analizie technicznej kursów akcji z giełdy papierów wartościowych. Analizując problematykę udzielania kredytów bankowych w kontekście zdolności kredytowej podmiotów czy też wystawiania polis ubezpieczeniowych – widać, że wszędzie występują wzorce.
Co zatem można rozpoznawać ? To już zależy od konkretnej potrzeby i zastosowania. Można rozpoznawać czy szum śrub napędowych okrętu podwodnego wskazuje na swój czy obcy ? Czy analiza danych dostarczonych przez klienta do banku potwierdzi jego wiarygodność jako kredytobiorcy ? do kompanii ubezpieczeniowej – jako ubezpieczanego na konkretnych warunkach ? Czy dana formacja techniczna budowana ze zmian na kilku ostatnich sesjach w połączeniu z inną, a może jeszcze z innymi pozwoli na wskazanie zmian kursów akcji w przyszłości ?
A dlaczego należy rozpoznawać ? Odpowiedź jest prosta. Wymienione wyżej przykładowe problemy charakteryzuje jedna cecha wspólna, o której wspominałem na początku. Wszystkie one nie mają rozwiązania algorytmicznego, a jeżeli ono nawet istnieje to dziś jest zbyt skomplikowane do znalezienia. Dlatego Sztuczne Sieci Neuronowe są w takich przypadkach niezastąpione.
Projektowanie i budowanie sieci
Jest to proces, od którego w oczywisty sposób zależy powodzenie użycia SSN do rozwiązywania postawionego problemu. Projektowanie sieci neuronowej zaczyna się już na poziomie analizy formułowanego zagadnienia. Mówiąc wprost, określenie jakie i ile danych chcemy lub możemy podać na wejścia sieci zdeterminuje wielkość warstwy wejściowej. Ilość wyjść sieci natomiast określi rodzaj oczekiwanej odpowiedzi czyli to, co spodziewamy się otrzymać na wyjściu. Pozostanie zatem do określenia ilość warstw ukrytych i neuronów w tych warstwach. Jest to najtrudniejszy moment tego etapu pracy. Przyjmuje się, że sieć z jedną warstwą ukrytą powinna nauczyć się rozwiązywania większości postawionych problemów. Nie znane są problemy wymagające do rozwiązania sieci z więcej niż trzema warstwami ukrytymi. Nie ma natomiast dobrej recepty na dobór właściwej ilości neuronów w warstwach ukrytych. Dla jednej takiej warstwy można próbować według wzoru:
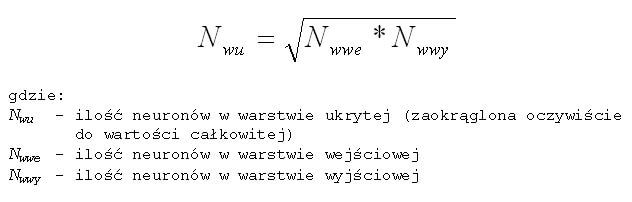
Przykład praktycznej implementacji tych wzorów zawiera listing 6. Rozwiązanie to oprócz wielu niewątpliwych zalet ma oczywiście i wady. Przy aplikacjach „odpornych” na naukę można próbować wykorzystać logarytm tego błędu.
Pierwszą czynnością w procesie uczenia jest przygotowanie dwóch ciągów danych: uczącego i weryfikującego. Ciąg uczący jest to zbiór takich danych, które w miarę dokładnie charakteryzują dany problem. Jednorazowa porcja danych nazywana jest wektorem uczącym. W jego skład wchodzi wektor wejściowy czyli te dane wejściowe, które podawane są na wejścia sieci i wektor wyjściowy czyli takie dane oczekiwane jednoznacznie zdeterminowane przez dane wejściowe, jakie sieć powinna wygenerować na swoich wyjściach. Pracę sieci rozpoczynamy zwykle od wygenerowania przypadkowych wartości współczynników wagowych (lub po prostu wag) przy neuronach
Przykładowy kod
/*** Generacja wag początkowych ***/
for(i=1;i<LW;i++)
for(j=0;j<n[i];j++)
for(k=0;k<=n[i-1];k++)
{
W[i][j][k] = (((rand() % 1000000L) / 1700.0) - 9.8)*0.0015;
if(W[i][j][k] == 0.0) W[i][j][k] = 0.01492;
}
/**********************************/
listing 1: generowanie przypadkowych wartości wag
Następnie aktywowane są wejścia sieci wektorem wejściowym i sygnały przetwarzane już przez wszystkie neurony sieci.
/*** Pojedyncze przetworzenie ***/
for(i=1;i<LW;i++)
for(j=0;j<n[i];j++)
{
I[i][j] = 0.0;
for(k=0;k<=n[i-1];k++)
I[i][j] += O[i-1][k] * W[i][j][k];
O[i][j] = 1.0 / (1.0 + exp(beta*(-I[i][j])));
}
/**********************************/
listing 2: przetwarzanie sygnału wejściowego w sieci
Po przetworzeniu wektora wejściowego, nauczyciel porównuje wartości otrzymane z wartościami oczekiwanymi i informuje sieć czy odpowiedź jest poprawna, a jeżeli nie, to jakie powstały błędy odpowiedzi (na każdym wyjściu sieci).
for(j=0;j<n[LW-1];j++)
B[LW-1][j] = Wy[wu][j] - O[LW-1][j];
/***********************************/
listing 3: błędy na wyjściach sieci
Błędy te są następnie propagowane do sieci ale w odwrotnej niż wektor wejściowy kolejności (od warstwy wyjściowej do wejściowej). W trakcie tego procesu, na każdym neuronie obliczany jest błąd tzw. delta (stąd nazwa – metoda delty) oznaczony w listingach jako E[i][j]:
/* Obliczanie błędów na neuronach */
/* warstwa wyjściowa */ i=LW-1;
for(j=0;j<n[i];j++)
E[i][j] = (Wy[wu][j]-O[i][j]) * O[i][j]*(1.0-O[i][j]);
/* warstwy ukryte */
for(i=LW-2;i>=1;i--)
for(j=0;j<n[i];j++)
{
E[i][j] = 0.0;
for(k=0;k<=n[i+1];k++)
E[i][j] += O[i][j]*(1.0-O[i][j]) * E[i+1][k] * W[i+1][k][j];
}
/**********************************/
listing 4: obliczanie błędów na każdym neuronie w sieci (wsteczna propagacja błędu)
Jak wynika z listingu 4 błąd delta na neuronie zależy od wartości pochodnych funkcji aktywacji każdego neuronu warstwy poprzedniej i wartości wag na połączeniach. Pamiętać należy, że przy propagacji wstecznej pierwszą jest warstwa wyjściowa.
Na podstawie tych błędów następuje taka adaptacja wag w każdym neuronie,
/********** Adaptacja wag *********/
for(i=1;i<LW;i++)
for(j=0;j<n[i];j++)
for(k=0;k<=n[i-1];k++)
{
W2[i][j][k] = W[i][j][k],
W [i][j][k] += eta * E[i][j] * O[i-1][k] + alfa*(W[i][j][k]-W1[i][j][k]),
W1[i][j][k] = W2[i][j][k];
}
/**********************************/
listing 5: adaptacja wag
aby ponowne przetworzenie tego samego wektora wejściowego spowodowało zmniejszenie błędu odpowiedzi. Procedurę tą powtarza się do momentu wygenerowania przez sieć błędu mniejszego niż założony. Wtedy na wejście sieci podaje się kolejny wektor wejściowy i powtarza te czynności. Po przetworzeniu całego ciągu uczącego (proces ten nazywany jest epoką) oblicza się błąd dla epoki
/***** Obliczanie błędu sieci *****/
for(j=0;j<n[LW-1];j++)
RMS += (Wy[wu][j] - O[LW-1][j])*(Wy[wu][j] - O[LW-1][j]);
ERMS = sqrt(RMS/(double)(ile_wek*n[LW-1]));
/*********************************/
listing 6: obliczanie błędu ERMS sieci dla pojedynczej epoki
i cały cykl powtarzany jest do momentu, aż błąd ten spadnie poniżej dopuszczalnego. Jak to już było zasygnalizowane wcześniej, SSN wykazują tolerancję na nieciągłości, przypadkowe zaburzenia lub wręcz niewielkie braki w zbiorze uczącym. Jest to wynikiem właśnie zdolności do uogólniania wiedzy.
c) Weryfikacja działania
Posiadając nauczoną już sieć, musimy zweryfikować jej działanie. W tym momencie ważne jest podanie na wejście sieci wzorców z poza zbioru treningowego w celu zbadania czy sieć może efektywnie generalizować zadanie, którego się nauczyła. Do tego używamy ciągu weryfikującego, który ma te same cechy co ciąg uczący to znaczy dane tak samo dokładnie charakteryzują problem i znamy dokładne odpowiedzi. Ważne jest jednak, aby dane te nie były używane uprzednio do uczenia. Dokonujemy zatem prezentacji ciągu weryfikującego z tą różnicą, że w tym procesie nie rzutujemy błędów wstecz a jedynie rejestrujemy ilość odpowiedzi poprawnych i na tej podstawie orzekamy, czy sieć spełnia nasze wymagania – czyli jak została nauczona. Orzekanie może być poparte analizą błędów, czasem bardzo rozbudowaną, np. statystyczną. Często tzw. Zbiór walidacyjny prezentowany jest w trakcie uczenia razem z ciągiem uczącym.
Wagi początkowe, z którymi sieć rozpoczyna naukę z reguły stanowią liczby wygenerowane przypadkowo. Po nauczeniu sieci, dla sprawdzenia otrzymanych wyników, należy kilkukrotnie powtórzyć całą procedurę poczynając od wygenerowania innych wag początkowych. Nigdy nie mamy bowiem gwarancji, że nawet prawidłowo zbudowana sieć nie utknęła w głębokim minimum lokalnym, podczas gdy interesuje nas znalezienie minimum globalnego.
Dla dużych sieci i ciągów uczących składających się z wielu tysięcy wektorów uczących, ilość obliczeń wykonywanych podczas całego cyklu uczenia jest gigantyczna a więc i czasochłonna. Nie zdarza się także aby sieć została dobrze zaprojektowana i zbudowana od razu. Zawsze zatem, o czym warto pamiętać aby uniknąć przykrych rozczarowań, osiągnięcie sukcesu jest efektem wielu prób i błędów.
Realizacja przykładowej sieci
Rozpoznawanie wzorców liter jest stosunkowo poważnym zadaniem do zrealizowania z wykorzystaniem sztucznej sieci neuronowej. Litery są utworzone na matrycy 5 x 7 czyli na 35 polach. I tyle wejść ma sieć. Ponieważ liter jest 26, prawidłowe rozpoznanie litery będzie polegało na uaktywnieniu jednego z 26 wyjść sieci, lub więcej w przypadku rozpoznawania w prezentowanym wektorze cech kilku liter. Zobaczymy jak znaleźć ilość neuronów w warstwie ukrytej oraz za pomocą jakich mechanizmów można sieć dostroić. Dopuszczalny poziom błędu sieci został ustalony na 0.01. Wszystkie dalsze dane oraz wykresy zostały wygenerowane i wykonane podczas uczenia opisanego przykładu.
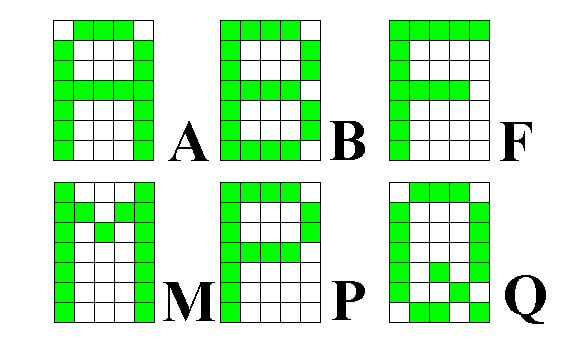
Rysunek 5: przykładowe wzorce liter A, B, F, M, P, Q
Matryce te należy skonwertować do postaci akceptowalnej przez sieć

Tabela 2: matryce 26 liter po konwersji zero-jedynkowej
Liniowym rozwinięciem tych matryc będą wektory wejściowe ciągu uczącego, który składa się z 26 wektorów uczących zbudowanych według schematu pokazanego poniżej tylko dla matryc liter z rysunku 6 (pozostałe tworzy się oczywiście tak samo):
Wektor wejściowy – 35 wartości
Wektor wyjściowy – 26 wartości
Identyfikator litery (tylko dla zobrazowania metody)
0 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 1 1 1 1 1 0 0 0 0 1 0 0 0 0 1 1 1 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 0 0 0 1 1 1 0 1 1 1 0 1 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 0 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Ustalając zatem wstępnie architekturę sieci na 35 – X – 26 rozpoczynamy uczenie z X = czterema neuronami w warstwie ukrytej (nu) i obserwując błąd sieci stopniowo zwiększamy ich ilość.

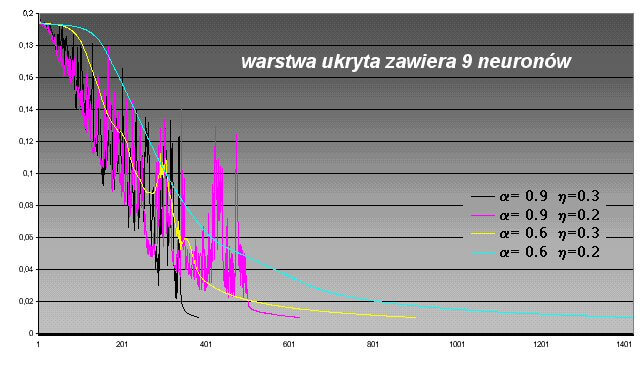
Jak widać na rysunku 6, dla 4, 5 i 6 takich neuronów sieć po osiągnięciu nawet 5000 epok nie zasygnalizowała chęci nauczenia. Sytuację diametralnie zmieniło dodanie siódmego neuronu. Sieć nauczyła się rozpoznawać przedstawione wzorce już po 488 epokach z tym, że całkowite nauczenie rozumiane jako sprowadzenie błędu sieci do wartości poniżej założonej (0.01) nastąpiło po 713 epokach. Dla 8 neuronów wartości te zmniejszyły się do odpowiednio 324 i 409 epok. Po dodaniu 9-go neuronu szybkość uczenia jeszcze wzrosła, choć znaczącego skoku już nie zaobserwowano. Zatem w dalszej analizie zostanie zbadane zachowanie sieci dla 9 neuronów w warstwie ukrytej. Proces uczenia jednak przebiega w sposób bardzo nierównomierny, widać gwałtowne oscylacje o bardzo dużej amplitudzie. Wskazuje to na duże skoki zmian wartości wagowych. Dla całego procesu istotne zaś jest, aby uczenie przebiegało płynnie. Dlatego algorytmy realizujące SSN wyposaża się mechanizmy dające projektantowi możliwość regulacji szybkości i jakości uczenia. Eliminują one gwałtowne zmiany czyli wygładzają przebieg funkcji błędu. W tym celu używa się współczynników: uczenia – eta, momentum – alfa oraz bias lub inaczej współczynnik stromości krzywej aktywacji – beta. Spójrzmy zatem na wzór, według którego następuje zmiana wag.
W[i][j][k] += eta * E[i][j] * O[i-1][k] + alfa * (W[i][j][k] – W1[i][j][k])
Współczynnik uczenia (eta) wpływa na szybkość uczenia poprzez bezpośrednie oddziaływanie na gradient zmiany. Zbyt duża jego wartość powoduje poruszanie się po wierzchołkach płaszczyzny błędu i pomijanie zagłębień z minimami. Zbyt mała wartość może spowodować utknięcie procesu uczenia w minimum lokalnym (rysunek 7). Znanych jest szereg technik pozwalających na dynamiczny dobór wartości tego współczynnika w zależności od aktualnego postępu w uczeniu, co pozwala na zminimalizowanie efektów niekorzystnych. Najczęściej stosowane wartości współczynnika uczenia zawierają się pomiędzy 0.01 a 0.6.
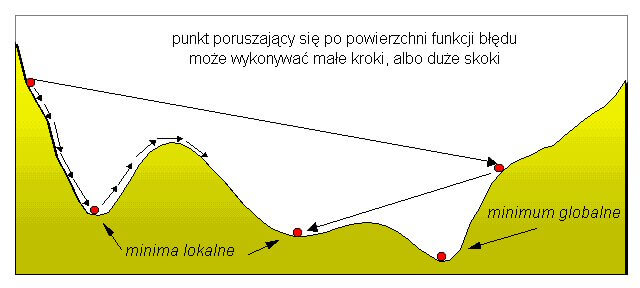
Aby uchronić się od gwałtownych zmian wartości wagowych, niekorzystnych dla uczenia, należy nadać procesowi zmian pewną bezwładność. W jej wyniku zmiana wag w bieżącym cyklu zależy również od zmiany jaka nastąpiła w cyklu poprzednim i pośrednio w cyklach jeszcze wcześniejszych. Bezwładność tę nadaje współczynnik momentum. Jak łatwo zauważyć, reguluje on wpływ zmiany wag na proces uczenia. Pomaga on także w opuszczeniu niegłębokich minimów lokalnych i poprawia efektywność uczenia w monotonicznych przedziałach funkcji energetycznej. Przyjmuje on wartości z przedziału 0 – 1, przy czy najczęściej stosowane to 0.5 – 1. Rysunek 8 pokazuje ich wpływ na wygląd wykresów funkcji błędów uczenia.
Spójrzmy teraz na wzór funkcji aktywacji neuronu (tutaj – sigmoidalnej):
O[i][j] = 1.0 / (1.0 + exp(beta*(-I[i][j])))
Współczynnik beta jak widać wpływa bezpośrednio na stromość funkcji aktywacji co skutkuje szybkością uczenia całej sieci. Może przyjmować wartości w przedziale 0.01 – 5.0; typowo 0.8 – 2.0
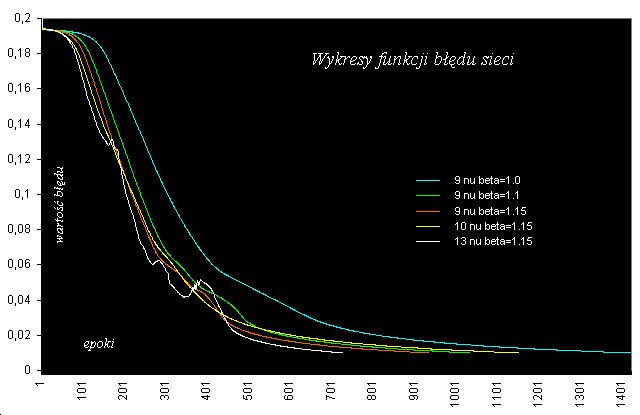
Na rysunku 9 przedstawiono wpływ współczynnika beta na szybkość i jakość procesu uczenia. Jak widać jego zwiększenie o 0.15 zmniejszyło ilość epok z 1423 do 937, ale też zakłóciło płynność w przedziale 0.06 – 0.02. W celu jej przywrócenia dodano jeden neuron w warstwie ukrytej. I właśnie sieć o architekturze 35 – 10 – 26 najlepiej rozpoznaje przedstawione wzorce liter (przy 1152 epokach). Proces uczenia przebiegł prawie idealnie. Aby sprawdzić jak sieć zareaguje na zwiększenie ilości neuronów w warstwie ukrytej, zbadano jej zachowanie dla 13. Wnioski pozostawiam czytelnikowi. Tak nauczona sieć prawidłowo rozpoznaje wzorce prezentowane do nauki, ale także doskonale sobie radzi z rozpoznawaniem liter zniekształconych. Podstawą oceny uczenia sieci jest jak widać bieżąca obserwacja błędu gdyż tak naprawdę to on pokazuje jak ten proces przebiega. Jednak zawsze istotnym jest zoptymalizowanie algorytmu przetwarzającego lub prowadzenie uczenia na szybkim komputerze, a najlepiej jest mieć te obie rzeczy na raz. Sprawdzeniem prawidłowości nauczenia sieci będzie rozwiązanie następującego problemu:
Zostaną wygenerowane wektory wejściowe, obrazujące ewolucję matrycy litery B do matrycy litery H tak, aby w pewnym momencie nastąpiło przybliżenie matrycy litery A. Wektorów takich będzie 12. Wyniki należy zinterpretować w ten sposób, że im większa będzie wartość liczbowa na wyjściu sieci odpowiadającemu danej literze, tym więcej cech danej litery w zaprezentowanej matrycy (wektorze wejściowym) sieć rozpoznała.
a) Otrzymane wyniki
W tabeli 3 zaprezentowano otrzymane wyniki. W pierwszej kolumnie pokazane są litery, a w odpowiadających im rzędach wartości, jakie uzyskano na wyjściach sieci prezentując jej wektor wejściowy wygenerowany na podstawie matrycy znaku pokazanego nad daną kolumną. Odcieniami szarości wyróżniono poziom rozpoznania cech litery.
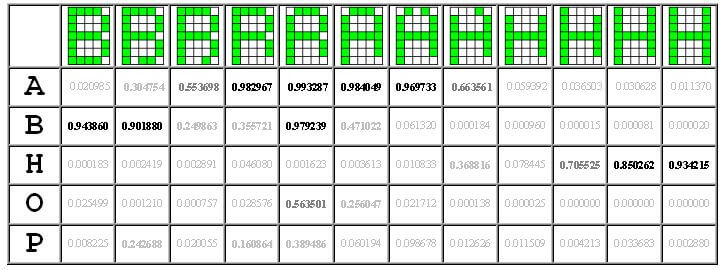
Nauczona sieć bardzo poprawnie rozpoznaje prezentowane wzory, nawet zniekształcone. Dostrzega w nich także i inne litery. Na tej podstawie można dokładnie badać jakie cechy liter zostały uznane przez siec za istotne.
Zwiększenie precyzji rozpoznawania liter czy też szerzej – wzorców znaków i symboli w prezentowanej sieci można uzyskać poprzez np. powiększenie rozmiarów matrycy i jednocześnie odpowiednio definiując okno dyskryminatora filtrującego wyniki.
Na podstawie przedstawionego przykładu można sformułować kolejne problemy w rozpoznawaniu wzorców znaków:
- powiększyć matryce znaków do np. 8 x 8, 9 x 14, 16 x 16 itp.
- rozszerzyć ciąg uczący o cyfry i narodowe znaki diakrytyczne
- dla pisma odręcznego, np. w polu o ściśle określonych rozmiarach (przykładem jest kod pocztowy wpisywany w kratki na kopertach listowych)
Liniowe rozwinięcie matryc oraz wyniki rozpoznawania znaków zakłóconych – dla wszystkich liter – można znaleźć na mojej stronie internetowej. Jest tam także szereg innych przykładów zastosowań SSN.
W podsumowaniu można się chyba pokusić o stwierdzenie, że trudne i pracochłonne projektowanie i uczenie SSN typu backpropagation powinno być uznane co najmniej w takim samym stopniu za sztukę jak i naukę. Nauka bowiem stworzyła teorię – podstawy matematyczne działania sieci. Natomiast sztuką jest umiejętność dokonania właściwego wyboru i przygotowania danych do wygenerowania ciągu uczącego oraz modelowanie współczynników mających wpływ na końcowy efekt. Wiele pakietów symulatorów SSN trafiło na półkę, ponieważ z powodu popełnienia przez użytkowników klasycznych błędów, nie przyniosło oczekiwanych efektów.
Na zakończenie należy wspomnieć o tym, że kolejnym krokiem dla wzrostu efektywności jest połączenie możliwości predykcji jaką posiadają sztuczne sieci neuronowe z przygotowaniem dla nich ciągów uczących za pomocą algorytmów genetycznych. W wyniku tego możliwości w przetwarzaniu danych ulegają zwielokrotnieniu. Wyobraźmy sobie mianowicie sytuację, w której za pomocą algorytmu genetycznego dobieramy taki wektor uczący zawierający np. zmodyfikowane genetycznie wskaźniki analizy technicznej akcji notowanych na giełdzie papierów wartościowych, aby sieć neuronowa, po przeprowadzonym procesie uczenia, wygenerowała w rozsądnym czasie informację o zmianie kursu akcji(indeksu) na sesji n+1, n+2, n+?. Ale to jest temat na zupełnie inną opowieść. Przyjęta konwencja oznaczeń w listingach – znaczenie poszczególnych zmiennych:
Pętle są realizowane od wartości początkowej 0 (nie od 1), dlatego indeksem oznaczającym warstwę wyjściową LW jest [LW-1].
Autorem tekstu jest Edward Chyliński
ps. wpis ma x lat powstanie okolice lat 2003-2004 😉


